§1.5 无穷小与无穷大

一、无穷小

1、无穷小的描述性定义

如果函数当(或) 时的极限为零，那么，称函数为(或) 时的无穷小。

2、无穷小的精确定义

，（或），当(或)时，有

成立，则称函数为当（或）时的无穷小，记作

无穷小并不是一个全新的概念，仅仅是在自变量的变化过程中，函数以零为极限。只是由于这类极限在高等数学中具有其特殊的地位，我们宁愿赋予它这一术语。

3、函数极限与无穷小的关系

【定理】

在自变量的同一变化过程 (或 )中，具有极限的函数等于它的极限与一个无穷小之和;

反之，如果函数可表示成常数与无穷小之和的形式， 则该常数就是函数的极限。

【证明】设， 依函数极限的定义有:

令 ， 则 是 时的无穷小，且

即等于它的极限 与一个无穷小 之和。

反过来，

设 ， 其中 是常数， 是 时的无穷小。

因 是时的无穷小， 依无穷小的定义有:

从而有 。

即 是当 时的极限。

( 类似地可证明 时的情形 )

二、无穷大

1、无穷大的描述性定义

如果函数当(或)时，其绝对值无限地增大，那么称函数为 (或) 时的无穷大。

2、无穷大的精确化定义

，（或 ），当 （或）时，有

成立，则称函数为当 （或 ）时的无穷大。

无穷大是一个全新的概念，对它的理解应注意如下几点:

(1)、据函数极限定义，若函数当(或)时为无穷大，那么函数的极限实际上是不存在的。但是为了描述函数的这一特别有用的性态，我们宁愿称函数的极限是无穷大，并记作

(2)、若将定义中换成，就记作

或

3、无穷小与无穷大的关系

【定理】

在自变量的同一变化过程（或 ）中，如果为无穷大，则为无穷小；

反之，如果为无穷小，且，则为无穷大。

这一定理所陈述的事实是显然的， 证明从略。

【例】试证明:

证明：，欲使，只需 ，

可取，当 时，有

成立，故。

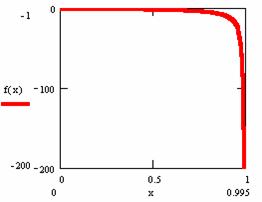
这一极限具有十分显著的几何特征，它表明:

直线是曲线的一条铅直渐近线。

用matlab作出该函数在区间[0，1]上的图形（事实上是[0，0.995]）上的图形，可以清楚地看出这一点。

不难将这一事实推广到一般

若，则直线 是曲线 的一条铅直渐近线。